ケリー基準（ケリーの公式） ウォーレンバフェットも使う投資サイズ判定法

※記事内に広告を含む場合があります

ケリー基準（ケリーの公式）とは、複利収益率が最も高くなる「最適な投資サイズ」を算出する方法です。

古くからギャンブルの世界では知られた手法でしたが、株式投資の世界でも応用可能であり、投資サイズの意思決定に使えます。

わかりやすく言うと、A社の株式に投資する時、全資産の何パーセントの資金量を投じるのが最も適切か？を判定してくれる計算式のことです。

真実は定かではありませんが、著名投資家のウォーレン・バフェットや、ピムコ創始者・債券王として有名なビル・グロスが使っているとも言われています。

私自身、ケリー基準（ケリーの公式）について深く学んでいるわけではなく、理解が曖昧な部分があると思います。

しかし今回は、私が学んだことをベースに、数学が苦手な方でもケリー基準（ケリーの公式）を使えるよう、可能な限り難しい数式を使わずに説明します。

もし、「間違っているよ」という意見がありましたらコメントにてお伝えいただけると嬉しく思います。

前置きが少し長くなりますが、

• ケリー基準がどういったものか？
• ケリー基準の計算方法

の順に解説していきます。

ケリー基準（ケリーの公式）とは？

ケリー基準とは、アメリカのベル研究所に在籍していたジョン・ラリー・ケリー・ジュニア（1923年 – 1965年）が1956年に考案した数式です。

ベル研究所には、天才的な科学者・数学者が数多く集まり、日々さまざまな研究を行っています。

当時、ベル研究所で最も頭がいいと言われていたのが、情報理論の父「クロード・シャノン」。次いで２番目に頭がいいと言われていたのが、ジョン・ケリーです。

ケリー基準を発見したジョン・ケリー自身は、賭け事をしませんでした。

しかし、この数式は後に、数学者・投資家であるエド・ソープがブラック・ジャックや株式市場で実践し、結果を出したことで広く知られるようになります。

ケリー基準・ケリーの公式・オプティマルfの違い

一般的には、

• ケリー基準（Kelly criterion）
• ケリーの公式（Kelly formula）
• オプティマルf

などと呼ばれます。

しかし上記の３つは完全に同じ意味ではなく、私の解釈では以下のようになりました。

重要なポイントですので、ゆっくり読み進めてください。

↓

↓

オプティマルfは、ラリー・ウィリアムズという著名トレーダーの書籍で解説されているようですが、私自身はこの本を読んでいません。

ラルフ・ビンズの「オプティマルf」は、主にFXやシステムトレードを利用する人が、ブログなどでよく言及している印象です。

今回の記事を書くにあたって、様々な書籍・ブログに当たりました。

その中で、「ケリー基準」「ケリーの公式」「オプティマルf」を同じ意味として解釈している人、違う意味だと解釈している人がいるように感じました。

また、書籍でも解説方法が異なっており、全体を通じて曖昧な印象を受けました。

しかし、様々な意見を総合的にまとめた結果

• ケリー基準（オリジナル）というシンプルな数式があり
• ケリーの公式やオプティマルfは、ジョン・ケリー考案の数式を発展させたものであり
• これらすべてを総称してケリー基準と呼ぶこともある

という解釈が最もしっくりくると考えています。

今回、ケリー基準の説明で私が参考にしたのは「天才数学者はこう賭ける―誰も語らなかった株とギャンブルの話」という書籍です。

よって、本書で示されている「ケリーの公式（f* = エッジ / オッズ）」について解説します。

上記の私の解釈では、「ケリーの公式」もケリー基準のひとつなのですが、話がわかりづらくなるので、以降は総称を「ケリー基準」、本記事で紹介する手法を「ケリーの公式」と呼びます。

ケリー基準を使う投資家

ケリー基準は多くのギャンブラーや投資家に使われています。

この公式を証明した「エド・ソープ」をはじめ、ウォーレン・バフェットや債券王ビル・グロスも、投資サイズの意思決定に用いていると言われています。

ただし、本人が使っていると言及したことはなく、また彼らが「ケリー基準（オリジナル）」「ケリーの公式」「オプティマルf」のどれを使って投資判断をしているのかも不明です。

しかし、彼らのポートフォリオから「厳選した少数に大きく賭ける」という本質的な部分は一致しています。

つまり、バフェットがケリー基準やケリーの公式を使っている、使っていないに限らず、「厳選した少数に大きく賭ける」という方法で資金マネジメントを行っているのは周知の事実であるということです。

ケリーの公式のメリット・デメリット

冒頭でも述べましたが、ケリーの公式で計算できるのは複利収益率が最も高くなる「最適な資金量（投資サイズ）」です。

投資もギャンブルも、確率が結果に影響を及ぼします。

勝てる確率と収益性を考慮した「期待値」がプラスにならない勝負には、そもそも手を出してはいけません。

しかし、期待値がプラスの勝負だからといって、１回の勝負で必ず勝てるとは限らないのです。

例えば、手持ちの資産が100万円、勝率70％で期待値もプラスになっている投資案件があったとします。

期待値がプラスなので、合理的な投資家であればこの投資案件に興味を示すでしょう。

しかし、１回の勝負で全財産である100万円を賭けてしまったら、、、もし30％の確率で発生する「負け」を運悪く引いてしまうと、一発で破産してしまいます。

逆に、保守的になりすぎて１万円しか賭けなかったら、もし勝ったとしてもリターンは限定されてしまいます。

では、リターンが最大になるリスクの取り方とはどのようなものなのか？これが、ケリーの公式が教えてくれる答えです。

ケリーの公式に従って賭け続ければ、もし賭けに負けて一時的に資金量が減っても、期待値がプラスである限り、いずれ必ず最高の複利収益率で資産が増加します。

その他のあらゆる賭け方よりも、ケリーの公式の賭け方が収益率が高くなることは、「天才数学者はこう賭ける」で詳しく説明されています。

ハーフケリーと部分ケリー

一方で、ケリーの公式にはデメリットもあります。

それは、ケリーの公式に従って賭けると「資産のボラティリティ（増減）が激しい」ため、心理的につらいということです。

「天才数学者はこう賭ける」のデータによれば、ケリーの公式に従って賭けると、資産が倍になる前に半分になる確率が３分の１あり、また資産が増えた後もそこから資産が半分になってしまう可能性も50％あるとのこと。

資産が50％以上減っても、ケリーの公式を信じきれるのであれば構いませんが、激しすぎる資産変動は気持ちのいいものではありません。

そこで多くのギャンブラーが好んで使っているのが、「半分ケリー（ハーフケリー）」という方法です。

ハーフケリーとは、ケリーの公式で導いた結果が「20％」だった場合、その半分の「10％」を賭けるという方法。

ケリーの公式に比べて複利収益率は４分の３に落ちますが、資産のボラティリティが抑えられることによって、資産が倍になる前に半分になる確率は９分の１に減少します。

もう一つの方法として、「部分ケリー」というやり方があります。

部分ケリーとは、全資産が100万円の場合でも、全資産が50万円と仮定してケリーの公式を実践するやり方です。

何冊かの本を読んでいる限りでは、このうち「ハーフケリー（計算結果の半分を賭ける）」の方が人気が高いと感じました。

期待値の見誤り

ケリーの公式のもう一つのデメリットは「エッジ（期待値）の見誤り」です。

ケリーの公式を実践するには、まず大前提として「期待値がマイナス（長期的に負ける）の勝負はしない」というものがあります。

株式投資の場合、勝てる確率や得られるリターンは、あくまでも投資家の「見積もり」に過ぎません。

エッジ（期待値）やオッズ（期待リターン）を見誤ってしまうと、ケリーの公式を使っても理想通りの利益は得られません。

エッジ・オッズが公開されているギャンブルならともかく、株式投資のような不確実な要素が多い勝負では、

• エッジ・オッズは保守的に見積もる
• ハーフケリーなどでリスクを抑える

という対策は必須であると思います。

私が参考にした書籍

今回の記事を書くにあたり、私が読んだ書籍の中から、ケリー基準についての言及がある書籍をまとめておきます。

ということで、前置きが長くなりました。

続いて本題であり、ケリーの公式の使い方について解説します。

ケリーの公式の使い方

ケリーの公式はとてもシンプルです。数学の知識がない方でも幅広く応用できます。

「f*」とは、ケリーの公式の計算結果です。

ケリーの公式を使って計算した結果、23％という数値が出たら投資可能な全資金量の23％をその銘柄に投資せよという意味です。

エッジとは？

「エッジ」とは、突き詰めて解釈すると「（収益と確率を考慮した）期待値」のことです。

期待値がプラスであれば、運の要素で一時的に負けることがあっても、回数を重ねるたびに、期待値通りの利益が得られます。

期待値がマイナスということは、運がよく一時的に勝てることがあっても、何度も勝負を重ねていくと、長期的には負けることを意味します。

ケリーの公式はまず第一に「期待値プラスである」ことが前提です。

オッズとは？

「オッズ」とは、私なりの解釈で突き詰めると勝った時に得られる最大利益のことです。（間違っているかもしれません）

書籍「ダンドー」では、「オッズ ＝ 価値の上限」、「オッズ ＝ 賭けの見込み」と表現しています。

また、書籍「天才数学者はこう賭ける」では、「オッズは５対１となっている。オッズは分数だ（５対１は5/1、つまり５だ。必要なのはこの５だけである）」と解説しています。

調べてみると、オッズには、

• フラクショナルオッズ（分数表記）
• デシマルオッズ（小数点表記）
• アメリカンオッズ（＋－表記）

の３つの種類があり、ギャンブルの種類や国によって表記が異なります。

書籍「天才数学者はこう賭ける」で説明されているのはこのうち、「フラクショナルオッズ」のことです。

オッズが５対１（５：１）となっている場合、１を賭けると５の利益が得られます。（賭け金とあわせて６の払い戻し）

そして、書籍「天才数学者はこう賭ける」では「５対１」のオッズのうち、ケリーの公式で必要なのは左側の「５」の数字だと言っており、これは勝った時に得られる利益と解釈できます。（もしかするとここは私の理解が間違っているかも知れないです）

株式投資においては、100円投資し300円で売却した場合、利益は200円なので、オッズを200とします。

勝ち負けのシナリオが複数ある場合、エッジ（期待値）は変化しますが、オッズは変わらず「勝った時に得られる最大利益」を使います。

このようにして、求めた「エッジ（期待値）」と「オッズ（利益）」を割り算することでケリーの公式による最適な投資比率が算出できます。

基本的なケーススタディ

この事例は、ケリーの公式を使った基本的な事例です。

オッズは「勝てばもらえる金額」なので２ドル。（勝った場合の返金額は３ドルです）

エッジは「期待値」なので、期待値の計算式「（利益 × 勝つ確率）＋（損失 × 負ける確率）」に基づいて、

(2ドル × 0.5) + (-1ドル × 0.5)

と計算します。計算結果は0.5になります。

最終的に、「エッジ/オッズ」に従って「0.5 / 2 ＝ 25％」がケリーの公式の導き出す数値です。

つまり、毎回全資産の25％を賭け続ければ、最速で資産が増加していきます。

勝ち負けシナリオが複数ある場合

この事例は、書籍「ダンドー」に示されていたものです。

オッズは「価値の上限」なので、21ドル

エッジは「期待値」なので、

(21ドル × 0.8) + (7.5ドル × 0.1) + (-1ドル × 0.1)

と計算します。計算結果は17.45になります。

最終的にエッジ（17.45） ÷ オッズ（21） ＝ 83％という結果になります。

つまり、この勝負では資産の83％を投じるべきであるということです。

株式投資への応用

株式投資への応用を考えてみます。

上記は書籍からの引用なので正しいはずですが、これは私のオリジナルの問題です。

もし間違っていたらコメントにてアドバイスをいただけるとたいへん助かります。

オッズは「価値の上限」なので、300円。

エッジは「期待値」なので、

(300円 × 0.2) + (100円 × 0.4) + (0円 × 0.3) + (-200円 × 0.1)

となり、計算結果は80です。

最終的に「80 ÷ 300 ＝ 26.6％」になりますから、この勝負では全資産の26.6％を投資するのがベストとなります。

ただし、株式投資の場合はボラティリティが大きいですから、ハーフケリーを用いて半分の「13.3％」を賭けてもよいでしょう。

ケリー基準の本質は賭けすぎないこと

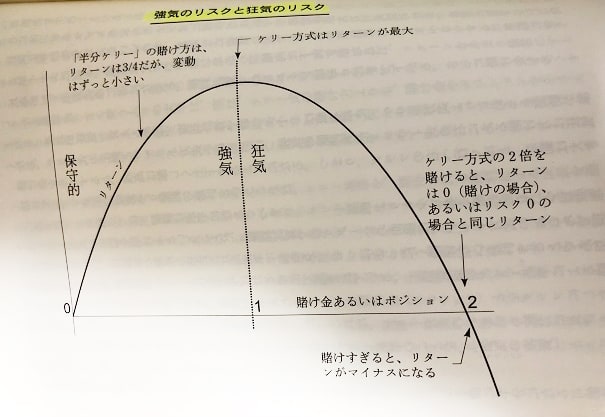
上記の画像は「天才数学者はこう賭ける」で示されている、リスクとリターンの相関図です。

ファイナンス理論では、リスクとリターンは比例すると考えられており、リスクを取れば取るほどリターンは大きくなると言われています。

これは正しい意見である一方、現実の世界では「限られた資金量で勝負しなくてはならない」という制限があります。

リスク・リターンは比例するからといって、目一杯のレバレッジをかけて勝負をすれば、かの有名なLTCM（ロングターム・キャピタル・マネジメント、1998年に事実上の破綻）のように一撃の失敗で破綻してしまいます。

ケリー基準はまさに、リスクの取りすぎ、取らなさすぎのギリギリのラインを算出するものです。

しかし現実では、期待通りのリターンが得られなかったり、期待値を見誤るといったことが起こります。

こうした内容を突き詰めて考えると、ケリー基準の示す本質は「決してケリー基準が示す値以上の資金を賭けないこと」だと思います。

私の理解が乏しいことも原因としてありますが、ケリー基準やケリーの公式の計算は曖昧な点が多いです。

書籍やブログなどを見てみても、計算方法・計算結果が人によって異なっていると思えるケースがたくさんありました。

しかし、その点は数学者でない私が追い求めるには時間がかかりすぎるため、現在の私自身の解釈をこの記事にまとめておくことにしました。

この記事の計算方法が誤っている可能性もありますが、私がケリーの公式から得られた３つの本質を述べて、この記事を締めくくりたいと思います。

• 厳選した少数に大きく賭ける
• ケリー基準が示す値を下回る資金量で勝負する
• 期待値がマイナスの場合は勝負しない

確実性が高い勝負では大きな資金量を投下し、自信がないときは少額の資金量にとどめます。

少なくとも、勝率100％でない限り「１つの投資対象に全額を投じることはありえない」ということです。（にもかかわらず多くの投資家がこれをやってしまっています）

２つめは、ケリー基準（ケリーの公式）が示した数値で勝負するのではなく、現実にはそれ以下で勝負するのが望ましいことです。

なぜなら、人は自分が想定した期待値・リターンを高く見積もりすぎることが往々にしてあるからです。

間違えても、ケリー基準を超える資金量で勝負をしてはなりません。

ケリー基準の数値を超えると、リスクを取るほどリターンが下がります。

最終的な結果は上記の図を見てもわかる通り、「最大のリスクでリターンがマイナス」つまり一撃で破綻することを意味します。

そして最後は、期待値がマイナスの場合は手を出さないことです。

取る必要のないリスクは取らないのが賢明です。

こちらの「期待値計算ツール」をお使いください。

次の記事：プロスペクト理論とは？投資に活かす方法、あなたの知らない心理学の世界

• P さんがコメントしました - 2023年12月18日
  決算書の「百万円」や「千円」の単位を素早く読む方法
• No Name さんがコメントしました - 2023年10月8日
  プロスペクト理論とは？投資に活かす方法、あなたの知らない心理学の世界
• DCF法くん さんがコメントしました - 2023年8月21日
  DCF法の世界一わかりやすい解説、割引率の決め方やエクセルでの計算方法
• No Name さんがコメントしました - 2023年8月19日
  DCF法シミュレーター
• にゃん太郎は長生き さんがコメントしました - 2023年6月19日
  証券マンがおすすめするファンドラップの評判を信じて買って良いのか